Graphs, Cuts and the Minimum Cut

Graphs

========

Introduction

In its most formal definition, A graph is a set of vertices and edges. In Computer science, it is a data type used to represent relationships or connections.

Examples: Road Networks, The Web, Social Networks, Precedence Constraints, Biological Structures, Computer chip design etc.

A Graph has two main ingredients:

• Vertices (set of vertices is represented by ‘V’ generally in Algorithms).
• Edges (pair of vertices, set of edges is represented by ‘E’ generally).
  
  

Types

There are two types of graphs mainly:

• Directed - A graph where the vertices are unordered pairs for a given edge.

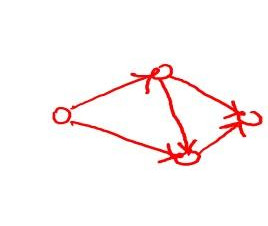
source: slide from Design and Analysis of Algorithms course by Tim Roughgarden on coursera.

• Undirected - When vertices are an ordered pair.

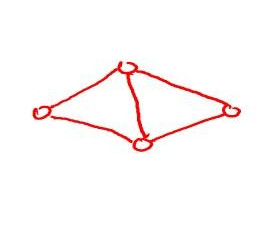
source: slide from Design and Analysis of Algorithms course by Tim Roughgarden on coursera.

So that was a sort of refresher to graphs for those who are familiar with it already. Those who are very unfamiliar with the term should consider reading about them first.

Cuts

=====

Definition

A cut is a partition of the vertices of a Graph into two non-empty sets A and B.

For example, if G(V, E) is a graph then a cut will devide V into two non-empty sets where some edges will remain in either A or B and some will cross the cut (crossing edges).

Examples:

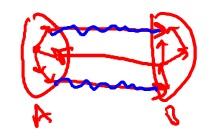
1. Directed Graph 2. Undirected Graph

source: slide from Design and Analysis of Algorithms course by Tim Roughgarden on coursera.

The Minimum Cut

===================

Problem Definition:

In Graph Theory, the minimum cut problem is to find a cut with minimum number of crossing edges.

Use of a Minimum Cut

There are many applications of the minimum cut. Few are listed below:

• Identifying Network Bottlenecks.
• Community detection in Social Networks.
• Image Segmentation.
• In recommendation systems.

How to find a minimum cut

Here is the Karger’s algorithm to compute a minimum cut in a given graph.

while number of vertices > 2:
    - pick a remaining edge(u, v) uniformly at random
    - merge u and v into a single vertex
    - remove self-loops
return cut represented by final 2 vertices

Now, I can’t share the code due to some reasons. But I will try to elaborate using pseudocode.

make adjacency list for the graph:
  graph = []
  for every vertex:V in graph:
    graph.append(V, all adjacent vertices of V) 

find min_cut:
  copy(graph)
  while length of graph > 2:

    choose a random index                : selecting random edge
    capture first and second element of index row 
    merge the captured elements into one : This is our contraction stage

    for every vertex:V in graph:
      if V[0] is the second captured element:
        remove the row for V 
      if first captured element in V:
        remove first captured element
      if second captured element in V:
        remove second captured element
      if first or second captured element were removed:
        V.append(merged vertex)

  pick the min(left two vertex lists):List
  for each element:E in List:
    sum(ocurrences of E)

  sum_of_occurences - len(List)

That’s it.

This will give the minimum number of cuts a given graph can have. The algorithm is randomized so it requires 3-4 continuous runs to find the exact answer. This algorithm can be used for many applications along with the few mentioned above.